The common denominator of my research is arithmetic geometry. Current subjects of focus include endomorphisms of Jacobians and Galois descent of curves and maps.
Publications
This is a list of my papers in reverse chronological order, with the arXiv identifier when available. Most of these have some calculation or implementation that goes with them. All these related programs can be found at my GitHub page or at Algorithms.
| 24. | [2104.04919] | Isogenous hyperelliptic and non-hyperelliptic Jacobians with maximal complex multiplication (with Bogdan Dina and Sorina Ionica), preprint available at arXiv:2104.04919, 28 pp. |
| 23. | [2102.04372] | Functionality for genus 2 and 3 curves (with Reynald Lercier and Christophe Ritzenthaler), preprint available at arXiv:2102.04372, 13 pp. |
| 22. | [2005.03587] | Gluing curves of genus 1 and 2 along their 2-torsion (with Jeroen Hanselman and Sam Schiavone), accepted by Mathematics of Computation, 41 pp. |
| 21. | [2003.07774] | Decomposing Jacobians via Galois covers (with Davide Lombardo, Elisa Lorenzo García, and Christophe Ritzenthaler), accepted by Experimental Mathematics, 31 pp. |
| 20. | [2003.06673] | Cubic function fields with prescribed ramification (with Valentijn Karemaker and Sophie Marques), accepted by International Journal of Number Theory, 24 pp. |
| 19. | [1908.00421] | A Prym variety with everywhere good reduction over $\mathbb{Q}(\sqrt{61})$ (with Nicolas Mascot and John Voight), accepted in Arithmetic Geometry, Number Theory and Computation (part of the Simons Symposia), 20 pp. |
| 18. | [1902.09624] | Conductor and discriminant of Picard curves (with Irene Bouw, Angelos Koutsianas, and Stefan Wewers), J. London Math. Soc. 102 (2020), Issue 1, 368-404. |
| 17. | [1807.02605] | Numerical computation of endomorphism rings (with Nils Bruin and Alexandre Zotine), in Proceedings of the Thirteenth Algorithmic Number Theory Symposium, 155–171, Open Book Ser., 2, Math. Sci. Publ., Berkeley, CA, 2019. |
| 16. | [1805.07751] | A database of Belyi maps (with Michael Musty, Sam Schiavone, and John Voight), in Proceedings of the Thirteenth Algorithmic Number Theory Symposium, 375–392, Open Book Ser., 2, Math. Sci. Publ., Berkeley, CA, 2019. Winner of the Selfridge Prize 2018 at ANTS-XIII. |
| 15. | [1707.01158] | Canonical models of arithmetic $(1; \infty)$-curves, in Arithmetic geometry: computation and applications, 149–165, Contemp. Math., 722, Amer. Math. Soc., Providence, RI, 2019. |
| 14. | [1705.09248] | Rigorous computation of the endomorphism ring of a Jacobian (with Edgar Costa, Nicolas Mascot and John Voight), Math. Comp. 88 (2019), no. 317, 1303–1339. |
| 13. | [1701.06489] | Plane quartics over $\Q$ with complex multiplication (with Pınar Kılıçer, Hugo Labrande, Reynald Lercier, Christophe Ritzenthaler and Marco Streng), Acta Arith. 185 (2018), no. 2, 127–156. |
| 12. | [1606.05594] | Reconstructing plane quartics from their invariants (with Reynald Lercier and Christophe Ritzenthaler), Discrete Comput. Geom. 63 (2020), no. 1, 73–113. |
| 11. | [1602.03715] | A database of genus 2 curves over the rational numbers (with Andrew Booker, Andrew Sutherland, John Voight and Dan Yasaki), LMS J. Comput. Math. 19 (2016), suppl. A, 235–254. |
| 10. | [1601.00126] | On some bounds for symmetric tensor rank of multiplication in finite fields (with Stéphane Ballet, Julia Pieltant and Matthieu Rambaud), in Arithmetic, geometry, cryptography and coding theory, 93–121, Contemp. Math., 686, Amer. Math. Soc., Providence, RI, 2017. |
| 9. | [1510.05601] | Distributions of traces of Frobenius for smooth plane curves over finite fields (with Reynald Lercier, Christophe Ritzenthaler, Florent Rovetta and Ben Smith), Exp. Math. 28 (2019), no. 1, 39–48. |
| 8. | [1504.02814] | On explicit descent of marked curves and maps, (with John Voight), Res. Number Theory 2 (2016), Art. 27, 35 pp. |
| 7. | [1403.0562] | Parametrizing the moduli space of curves and applications to smooth plane quartics over finite fields (with Reynald Lercier, Christophe Ritzenthaler and Florent Rovetta), fields. LMS J. Comput. Math. 17 (2014), suppl. A, 128–147. |
| 6. | [1311.2529] | On computing Belyi maps (with John Voight) Publ. Math. Besançon Algèbre Théorie Nr., 2014/1, Presses Univ. Franche-Comté, Besançon, 2014. |
| 5. | [1301.0695] | Explicit Galois obstruction and descent for hyperelliptic curves with tamely cyclic reduced automorphism group (with Reynald Lercier and Christophe Ritzenthaler), Math. Comp. 85 (2016), no. 300, 2011–2045. |
| 4. | [1211.1327] | An explicit expression of the Lüroth invariant (with Romain Basson, Reynald Lercier and Christophe Ritzenthaler), ISSAC 2013—Proceedings of the 38th International Symposium on Symbolic and Algebraic Computation, 31–36, ACM, New York, 2013. |
| 3. | [1203.5440] | Fast computation of isomorphisms of hyperelliptic curves and explicit descent (with Reynald Lercier and Christophe Ritzenthaler), ANTS X—Proceedings of the Tenth Algorithmic Number Theory Symposium, 463–486, Open Book Ser., 1, Math. Sci. Publ., Berkeley, CA, 2013. |
| 2. | [PDF] | Canonical models of arithmetic (1;e)-curves, Math. Z. 273 (2013), no. 1-2, 173–210. |
| 1. | [PDF] | Arithmetic (1;e)-curves and Belyi maps, Math. Comp. 81 (2012), no. 279, 1823–1855. |
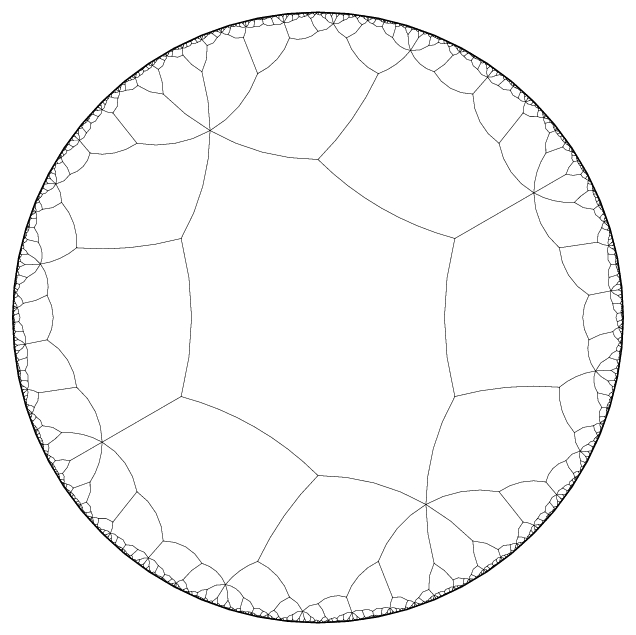
Thesis: Equations for arithmetic pointed tori
My Ph.D. thesis is concerned with the following questions:
- Calculating Belyi maps associated with arithmetic Fuchsian groups commensurable with a triangle group;
- Finding equations for arithmetic curves of genus 1 with a single elliptic point;
- Explicitly calculating dual graphs for Shimura curves at primes dividing the discriminant of the associated quaternion algebra.
It is in this context that the Escher-like tiling of the disc on the right made its appearance. You can click here to download the thesis as submitted at the time. It contains a somewhat broader and chattier exposition on Shimura curves. Experts may prefer the articles above.
History of interests
As a Ph.D student in Utrecht under the supervision of Frits Beukers, my research was centered around explicit aspects of Shimura curves. More on this can be found in my thesis; on the right, a Dirichlet domain for a genus 1 Shimura curve with a single elliptic point of order 3 is given.
I remain interested in the following questions centered around Shimura curves:
- Finding algorithmic methods to determine the correctness of a conjectural equation;
- Finding necessary and sufficient conditions on a Belyi map to arise from an inclusion of arithmetic Fuchsian groups that are congruence;
- Finding a way to bring the power of p-adic geometry and p-adic differential equations to bear on Lamé equations, both for determining accessory parameters and to compare the monodromy groups in the classical and the p-adic situations.
I have been fortunate enough to work on these questions at the MPI in Bonn and after that at the IMPA in Rio de Janeiro (on invitation of Hossein Movasati).
After these projects, I spent a year at the IRMAR in Rennes in the context of Project CHIC. This research, conducted together with Reynald Lercier and Christophe Ritzenthaler, was concerned with covariants and their applications to hyperelliptic and plane curves, as well as the problem of Galois descent, which we managed to solve completely for hyperelliptic curves. Furthermore, together with Romain Basson we managed to solve a century-old problem on plane quartics admitting an inscribed pentalateral, as well as disproving an equally old conjecture due to Morley.
This period in France was followed by a Marie Skłodowska-Curie grant, funded by the European Commission, with Samir Siksek at the University of Warwick. Its theme was a project on dessins d'enfants, and was thus close to the subject of my master's thesis, written under the supervision of Jaap Top. The project was concerned with dessins as a subject in itself, but in fact dessins and more general covers are intimately related with many areas of mathematics. For example, the question of Galois descent for hyperelliptic curves mentioned above shows that even the theory of degree 2 covers of the projective line is already very rich from an arithmetic point of view. Work with Musty, Schiavone, and Voight describes a database of Belyi maps over the rationals, as well as the Galois descent problem for Belyi maps.
Before coming to Ulm, I worked at Dartmouth College with John Voight on many questions related to computational aspects of curves. This included both the aforementioned themes of descent and dessins, but also dealt with other questions, such as computational aspects modularity and endomorphisms of Jacobians of curves of small genus, a project culminating in a joint work with with Edgar Costa and Nicolas Mascot. Its theme was also considered in another article with Nils Bruin and Alexandre Zotine. Some of these results and algorithms have been included in the genus 2 part of the LMFDB.
More recently Lercier, Ritzenthaler and I again took up the subject of invariants of curves and we managed to write algorithms to reconstruct a plane quartic from given Dixmier-Ohno invariants. The corresponding preprint can be found above; in a broader collaboration with Pınar Kılıçer, Hugo Labrande and Marco Streng, we used these algorithms to find plane quartics over $\Q$ with complex multiplication.
I am generally interested in curves of small genus and their arithmetic aspects; a more recent preprint on this topic concerns a database of Picard curves, constructed with my colleagues Irene Bouw, Angelos Koutsianas and Stefan Wewers from Ulm. Curves of low genus and their Parshin fibrations also play a part in a work on cubic function fields writte in collaboration with Valentijn Karemaker and Sophie Marques.
Recent years saw further contact with Lercier, Ritzenthaler, as well as with Davide Lombardo Davide Lombardo and Elisa Lorenzo García, in the context of a PICS (JADERE) sponsored by the French CNRS, which has so far among other results led to explicit algebraic techniques for decomposing Jacobians using suitable Galois closures.
The inverse of this decomposition process, namely the gluing of Jacobians of curves to Jacobians and general abelian varieties of higher genus, played a role in a the Juniorprofessuren-Programm "Endomorphismen algebraischer Kurven" project funded by the Science Ministry of Baden-Württemberg. Not only did this project lead to results on Prym varieties with everywhere good reduction over over $\mathbb{Q}(\sqrt{61})$ obtained in collaboration with Mascot and Voight, but it also made the PhD results of Jeroen Hanselman possible. His work furnishes methods for gluing the Jacobians of curves of genus 1 and 2. The main results of this research, as well as optimizations and further developments, were submitted in a collaboration with Sam Schiavone.
I remain interested in basically any questions concerning automorphisms of curves and Galois descent of varieties and dessins, also in positive characteristic. Results obtained so far on Galois descent seem to suggest that there is a more formal theory building on Galois cohomology that would explain their surprising simplicity, a subject that my students and I will consider, along with corresponding implementation, in the context of a recently awarded DFG Individual Research Grant "Abstieg algebraischer Kurven".